Leetcode: #235 Lowest Common Ancestor of a Binary Search Tree

Since I’m doing Leetcode daily, I though it’d be cool to start doing writeups on some of the problems I’ve worked on.

This is a basic binary search tree problem. The problem statement is as follows:

Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

What does this mean exactly?

In plain English, it means that we must figure out which (out of p and q) is the largest (max), as well as the smallest (min). Then, we must search the tree and return the node between the nodes that hold these values.

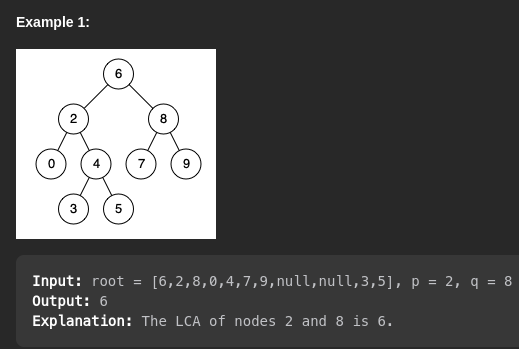
A visual example:

See how the output is 6, and how that node was the ancestor of the nodes holding the values 2 and 8?

This is what the Lowest Common Ancestor is, or LCA for short.

To do this we’ll use a variation of the Depth First Search algo to recurse along the tree until we find the node we’re looking for…the one between the min/max values of the tree. Its extremely similar (or perhaps, it is) to Binary Search.

I’ve commented the code to make it easier to understand:

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        # Get the min/max values for P and Q at the root
        self.min_val = min(p.val, q.val)
        self.max_val = max(p.val, q.val)

        # Recursive util
        def go(root):
			# Base Case
            # If we reach the end of the list (when root is None), return None
            if not root:
                return root
			
			# Recursive Case
            # If the current node's value is larger than max_val
            if root.val > self.max_val:
                # Return result of recursing to left
                return go(root.left)
            
			# Recursive Case
            # If the current node's value is smaller than min_val
            if root.val < self.min_val:
                # Return result of recursing to right
                return go(root.right)

            # At the very end, the only node returned should be between the nodes holding p and q
            # which means it is the LCA
            return root
        
        # Return result of util
        return go(root)

Now, you might ask yourself. Why is it that we don’t ever update the min or max as we go through the tree?

Remember the properties of a binary search tree.

In a BST or binary search tree, all nodes to the right of the current node are larger than the current node. All nodes to the left, smaller.

We exploit this property using DFS/binary search above. Hope this was helpful!

Be excellent to each other,

• L